
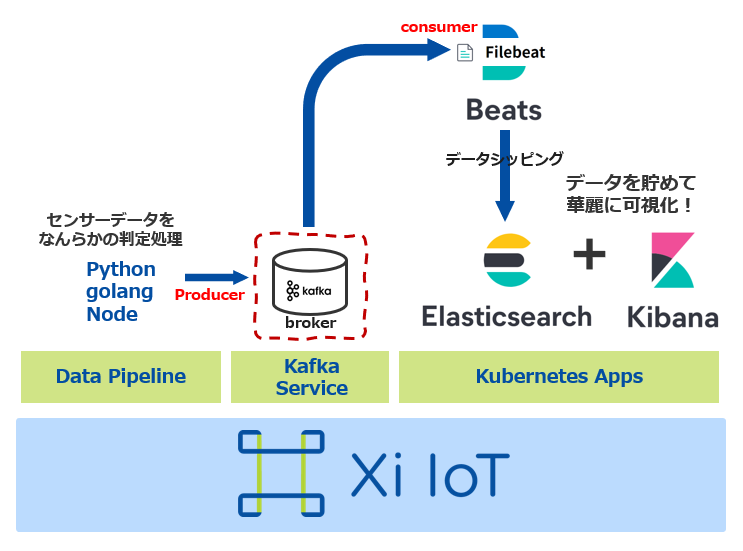

"Utility-Consistent Brand Demand Systems with Endogenous Category Consumption: Principles and Marketing Applications". "Monopolistic Competition and Optimum Product Diversity".
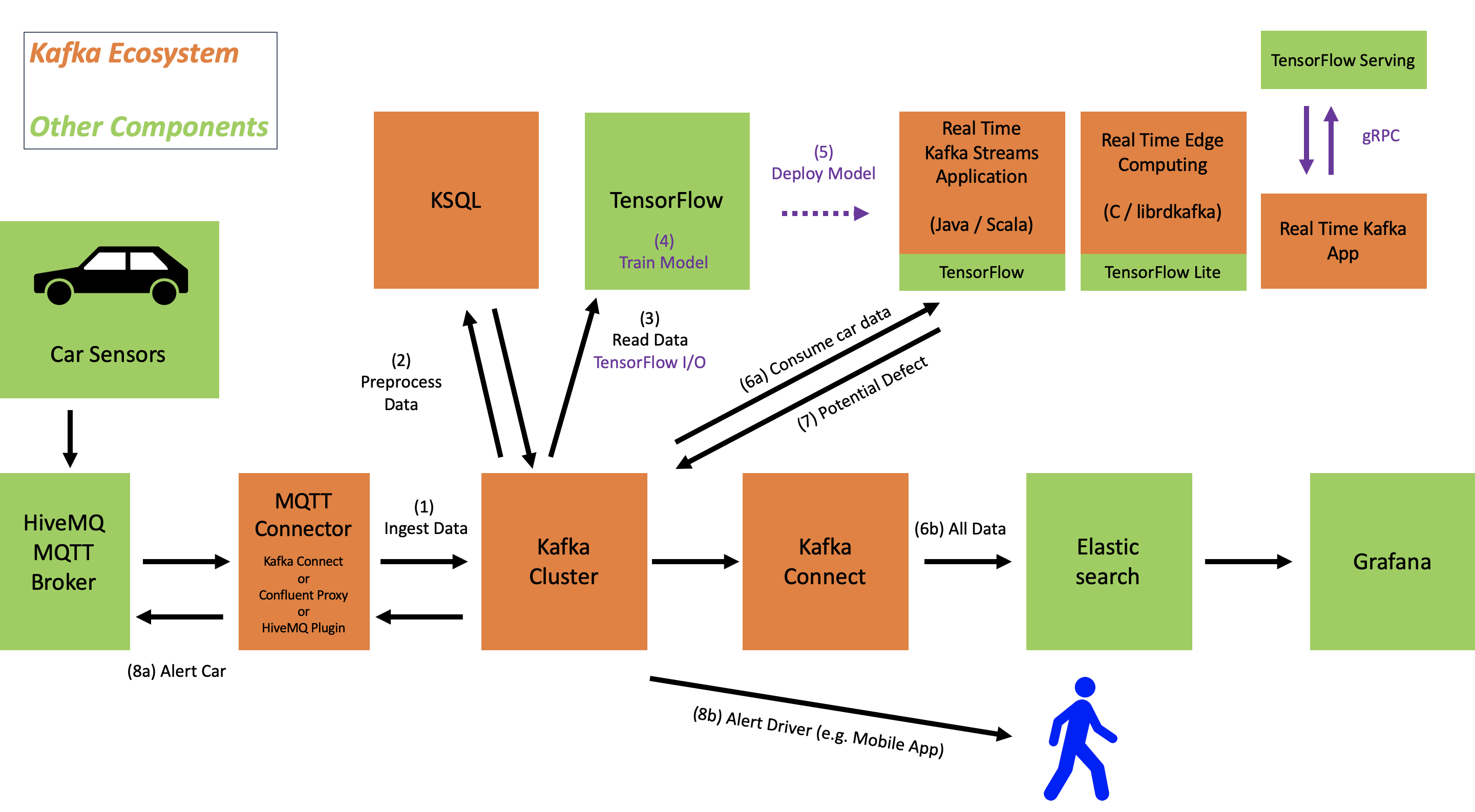
^ Dixit, Avinash Stiglitz, Joseph (1977)."A theory of demand for products distinguished by place of production". "Production functions with constant elasticities of substitution". "Factor Substitution and Factor Augmenting Technical Progress in the US: A Normalized Supply-Side System Approach". 1: Econometric Modelling of Producer Behavior. "Capital-labor substitution and economic efficiency". "A contribution to the theory of economic growth". "Constant Elasticity of Substitution Production Functions". It has also been shown that CES preferences are self-dual and that both primal and dual CES preferences yield systems of indifference curves that may exhibit any degree of convexity. A CES indirect (dual) utility function has been used to derive utility-consistent brand demand systems where category demands are determined endogenously by a multi-category, CES indirect (dual) utility function. Note the difference between CES utility and isoelastic utility: the CES utility function is an ordinal utility function that represents preferences on sure consumption commodity bundles, while the isoelastic utility function is a cardinal utility function that represents preferences on lotteries. The two factor (capital, labor) CES production function introduced by Solow, and later made popular by Arrow, Chenery, Minhas, and Solow is: Q = F ⋅ ( a ⋅ K ρ + ( 1 − a ) ⋅ L ρ ) υ ρ Ī CES utility function is one of the cases considered by Dixit and Stiglitz (1977) in their study of optimal product diversity in a context of monopolistic competition. labour and capital) proportions due to a percentage change in marginal rate of technical substitution. In other words, the production technology has a constant percentage change in factor (e.g. The CES production function is a neoclassical production function that displays constant elasticity of substitution. This has been done by Arrow-Chenery-Minhas-Solow for the two-factor production case. The constant E.S assumption is a restriction on the form of production possibilities, and one can characterize the class of production functions which have this property. On the contrary of restricting direct empirical evaluation, the constant Elasticity of Substitution are simple to use and hence are widely used. Despite having several factors of production in substitutability, the most common are the forms of elasticity of substitution.


 0 kommentar(er)
0 kommentar(er)
